INVERSE SQUARE LAW |
| Another very important
but little known acoustical phenomena is the Inverse Square Law. As a
sound wave propagates spherically, the sound energy is distributed over
the ever-increasing surface diameter of the wave front surface. The Inverse
Square Law teaches us that for every doubling of the distance from the
sound source in a free field situation, the sound intensity will diminish
by 6 decibels. Under ideal conditions a free field could be represented by a sound signal being generated from a mountain peak. In real life situations however, rooms bounded by walls, floors and ceilings will interrupt the inverse square law at a distance in tan average 30' square room at approximately 10-12 feet from the sound source. Nevertheless it is important to accept the notion that sound will diminish in intensity with distance. For example, in a typical classroom with a teachers voice signal of 65 decibels at a three-foot distance from the teacher; at 6 feet away the sound intensity will be 59 decibels and at twelve feet it will diminish down to 53 decibels. (This is important to remember as we discuss the Signal to Noise Ratio S/NR later on) (FIGURE 8) shows a segment of the sound wave front surface area increasing with distance. 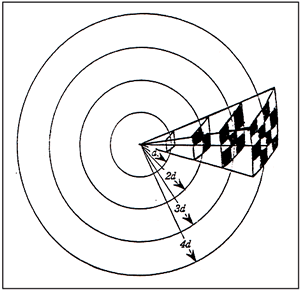 (FIGURE
8) (FIGURE
8)In the angle shown in Figure 8, the same sound energy is distributed over the spherical surfaces of increasing areas a s d is increased. The intensity of the sound is inversely proportional to the square of the distance of the wavefront from the signal source. Example: 1d = 1 2d = 4 3d = 9 4d = 16 |